COBYQA documentation#
- Version:
1.1
- Useful links:
- Authors:
COBYQA is a derivative-free optimization solver designed to supersede COBYLA. Using only functions values, and no derivatives, it aims at solving problems of the form
where \(\mathcal{X} = \{ x \in \mathbb{R}^n : l \le x \le u \}\). COBYQA always respect the bound constraints throughout the optimization process. Hence, the nonlinear functions \(f\) and \(c\) do not need to be well-defined outside \(\mathcal{X}\). In essence, COBYQA is a derivative-free trust-region SQP method based on quadratic models obtained by underdetermined interpolation. For a more detailed description of the algorithm, see the framework description.
To install COBYQA using pip, run in your terminal
pip install cobyqa
If you are using conda, you can install COBYQA from the conda-forge channel by running
conda install conda-forge::cobyqa
For more details on the installation and the usage of COBYQA, see the user guide.
Citing COBYQA#
If you would like to acknowledge the significance of COBYQA in your research, we suggest citing the project as follows.
T. M. Ragonneau. “Model-Based Derivative-Free Optimization Methods and Software.” PhD thesis. Hong Kong, China: Department of Applied Mathematics, The Hong Kong Polytechnic University, 2022. URL: https://theses.lib.polyu.edu.hk/handle/200/12294.
T. M. Ragonneau and Z. Zhang. COBYQA Version 1.1.1. 2024. URL: https://www.cobyqa.com.
The corresponding BibTeX entries are given hereunder.
@phdthesis{rago_thesis,
title = {Model-Based Derivative-Free Optimization Methods and Software},
author = {Ragonneau, T. M.},
school = {Department of Applied Mathematics, The Hong Kong Polytechnic University},
address = {Hong Kong, China},
year = 2022,
url = {https://theses.lib.polyu.edu.hk/handle/200/12294},
}
@misc{razh_cobyqa,
author = {Ragonneau, T. M. and Zhang, Z.},
title = {{COBYQA} {V}ersion 1.1.1},
year = 2024,
url = {https://www.cobyqa.com},
}
Statistics#
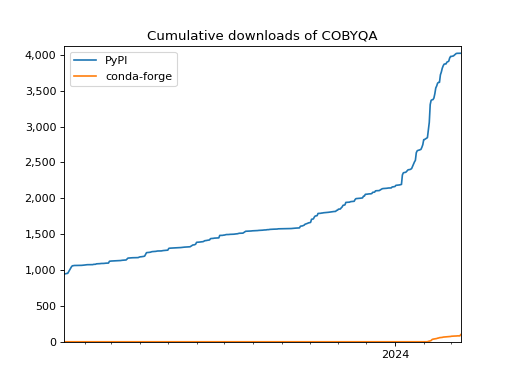
As of March 12, 2024, COBYQA has been downloaded 4,121 times, including
4,021 times on PyPI (mirror downloads excluded), and
100 times on conda-forge.
The following figure shows the cumulative downloads of COBYQA.
(Source code, png, hires.png, pdf)
Acknowledgments#
This work was partially supported by the Research Grants Council of Hong Kong under Grants PF18-24698, PolyU 253012/17P, PolyU 153054/20P, PolyU 153066/21P, and The Hong Kong Polytechnic University.